 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
设随机变量X服从参数为λ=1的指数分布,试求E[max(X,2)]与E[min(X,2)).
设随机变量X服从参数为λ=1的指数分布,试求E[max(X,2)]与E[min(X,2)).
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
设随机变量X服从参数为λ=1的指数分布,试求E[max(X,2)]与E[min(X,2)).
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“设随机变量X服从参数为λ=1的指数分布,试求E[max(X,…”相关的问题
更多“设随机变量X服从参数为λ=1的指数分布,试求E[max(X,…”相关的问题
设 为独立同分布的随机变量序列,且均服从参数为λ(λ>1) 的指数分布,记φ(x)为标准正态分布函数,则有()
为独立同分布的随机变量序列,且均服从参数为λ(λ>1) 的指数分布,记φ(x)为标准正态分布函数,则有()
A.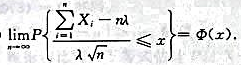
B.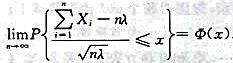
C.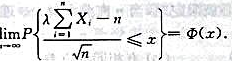
D.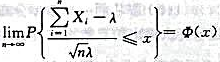
设随机变量X与Y相互独立,且X在区间[0,2]上服从均匀分布,Y服从参数为3的指数分布,则数学期望E(XY)等于()。
A.4/3
B.1
C.2/3
D.1/3
设随机变量X服从参数为2的指数分布,则下列各项中正确的是()
A.E(X)=0.5,D(X)=0.25
B.E(X)=2,D(X)=2
C.E(X)=0.5,D(X)=0.5
D.E(X)=2,D(X)=4
设顾客在某银行的窗口等待服务的时间X(单位:min)是一随机变量,它服从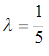 的指数分布,其密度函数为
的指数分布,其密度函数为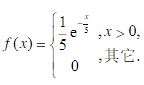 某顾客在窗口等待服务,若超过10min,他就离开.
某顾客在窗口等待服务,若超过10min,他就离开.
(1)该顾客某天去银行,求他未等到服务就离开的概率;
(2)设该顾客一个月要去银行五次,求他五次中至多有一次未等到服务而离开的概率