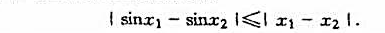题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
[主观题]
(1)证明:对任意的mxm矩阵A,ATA和AAT都是对称矩阵。(2)证明:对任意的n阶矩阵A,A+AT为对称矩阵,而A-AT为反称矩阵。
(1)证明:对任意的mxm矩阵A,ATA和AAT都是对称矩阵。(2)证明:对任意的n阶矩阵A,A+AT为对称矩阵,而A-AT为反称矩阵。
查看答案
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“(1)证明:对任意的mxm矩阵A,ATA和AAT都是对称矩阵…”相关的问题
更多“(1)证明:对任意的mxm矩阵A,ATA和AAT都是对称矩阵…”相关的问题
证明:设A,B都是n阶正交方阵,则
(1)|A|=1或-1(2)AT,A-1,AB也是正交方阵。
(2) A正交方阵,得ATA=E,由AAT=E得AT正交方阵。又A-1=AT, 故A-1正交方阵。A,B是n阶正交矩阵,故A-1=AT,B-1=BT。(AB)T(AB) =BTATAB=B-1A-1AB=E, 故AB也是正交方阵。
设x=(x1,...,xn)T是不可约对称三对角矩阵
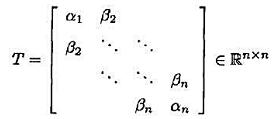
对应于特征值λ的特征向量。证明:
(1)x1xn≠0;
(2)若取x1=1,则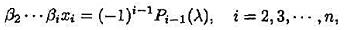 其中Pi(λ)由(6.64)定义。
其中Pi(λ)由(6.64)定义。
n维欧氏空间V的一个线性变换σ说是反对称的,如果对于任意向量a,β∈V。
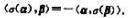 证明:
证明:
(i)反对称变换关于V的任意规范正交基的矩阵都是反对称的实矩阵(满足条件AT=-A的矩阵叫作反对称矩阵);
(ii)反之,如果线性变换σ关于V的某一规范正交基的矩阵是反对称的,那么σ一定是反对称线性变换;
(iii)反对称实矩阵的特征根或都是零,或者是纯虚数。
证明:(1)若函数f在[a,b]上可导,且f'(x)≥m,则
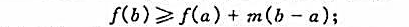
(2)若函数f在[a,b]上可导,且
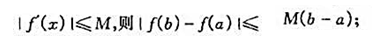
(3)对任意实数x1,x2,都有