 更多“用极限定义直接证明教材中定理3的推论2.”相关的问题
更多“用极限定义直接证明教材中定理3的推论2.”相关的问题
证明定理16.3.2的推论16.3.1: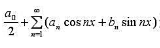 是某个可积或绝对可积函数的Fourier级数的必要条件是
是某个可积或绝对可积函数的Fourier级数的必要条件是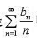 收敛。
收敛。
设有函数序列fn(x)(a≤x≤b,n=1,2,...证明:
(1)若每一个函数fn(x)都在区间[a,b]上连续,而丽数序列fn(x)在[a,b]上一致收敛于极限函数f(x),则函数f(x)在区间[a,b]上也连续,且

(2)若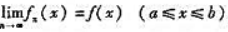 ,又每一个函数fn(x)都有连续的导数f'n(x),且导函数列f'n(x)在区间[a,b]上一致收敛,则极限函数f(x)在区间[a,b]上也有连续的导数f'(x),且
,又每一个函数fn(x)都有连续的导数f'n(x),且导函数列f'n(x)在区间[a,b]上一致收敛,则极限函数f(x)在区间[a,b]上也有连续的导数f'(x),且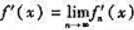 ,即
,即
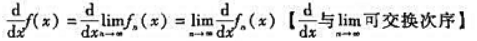
[可以直接证明,也可以利用函数项级数的相应结论来证明]
利用PHILLIPS.RAW中的数据。
(i)用直至1997年的数据估计教材(18.48)和(18.49)中的模型。参数估计值与教材(18.48)和教材(18.49)中的结果相比有很大不同吗?
(ii)用新方程预测unem1998,小数点后保留两位数。哪个方程预测得更好?
(ii)我们在正文中讨论过,用教材(18.49)预测unem1998为4.90.把它与利用直至1997年的数据得到的预测相比较。多用一年数据求得的参数估计值能给出更好的预测吗?
(iv)用教材(18.48)中估计的模型求出unem的提前两期预测值。即利用α=1.572,p=0.732,h=2时的教材方程(18.55)预测unem与把unem1997=4.9代入教材(18.48)所得到的提前一期预测值相比,哪一个更好?
用到MROZ.RAW中的数据。
(i)用log(hours)作为因变量重新估计教材例16.5中的劳动供给函数。将估计出的弹性(现在是常数)与教材方程(16.24)在平均工作小时数处所得到的估计值相比较。
(ii)在第(i)部分的劳动供给方程中,容许educ因遗漏了能力变量而成为内生变量。用motheduc和fatheduc作为educ的Ⅳ。记住,你现在在方程中有两个内生变量。
(iii)检验第(ii)部分2SLS估计中过度识别约束。这些Ⅳ通过检验了吗?
(i)利用WAGEPRC.RAW中的数据,估计第11章习题5中的分布滞后模型。用回归教材(12.14)来检验AR(1)序列相关。
(ii)用迭代的科克伦-奥卡特方法重新估计这个模型。长期倾向的新估计值是多少?
(iii)用迭代C0求出LRP的标准误。(这要求你估计一个修正方程。)判断LRP估计值在5%的水平上是否统计显著异于1?


 如果结果不匹配,请
如果结果不匹配,请 
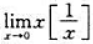 ,其中
,其中 的取整函数,提示:当x≠0时,
的取整函数,提示:当x≠0时,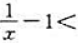
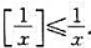
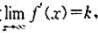 求
求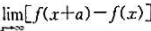 ,
,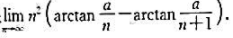
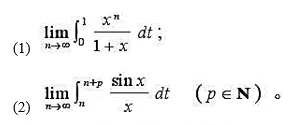
 定义中的N是不是ε的函数?
定义中的N是不是ε的函数?















